VIDEO DE CONICAS

NOCHES DE ESTUDIO DC

Hola a todos, ahora una pequeñísima clase de cónicas, usando unos conos de helado para el ejemplo, que lo disfruten y que viva a Ringo Starr.

PENDIENTE

NOCHES DE ESTUDIO DC

 Hola que tal amigos el día de hoy veremos un tema muy importante es un placer ayudarlos y resibirlos en nuestra página web , bueno comenzemos

Pendiente 

Se denomina pendiente a la inclinación de un elemento lineal, natural o constructivo respecto a la horizontal .
En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento lineal, natural o constructivo respecto de la horizontal (de 0° o 180°).

En geometría analítica, puede referirse a la pendiente de la ecuación de una recta (o coeficiente angular)como caso particular de la tangente a una curva, en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante, por ejemplo, en el trazado altimétrico de carreteras, vías férreas o canales.

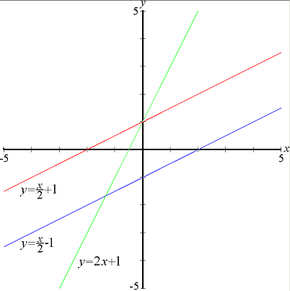
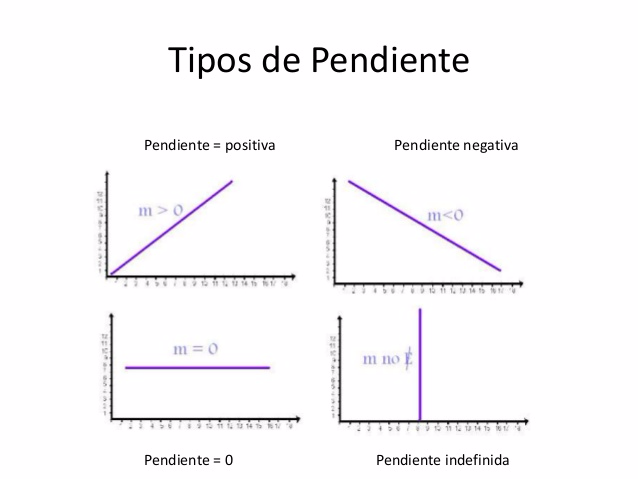
Tenemos tipos de pendientes , como lo indica la gráfica

Aca le dejo unos ejemplos que nos ayudarán a realizar nuestros ejercicios:

Ejemplo 1:

https://www.youtube.com/watch?v=ULxjPNTiAZ8

Ejemplo 2:

https://www.youtube.com/watch?v=pmW_RHPRRUY

¿Cuales son los objetivos de esta clase de pendiente?

Asi que si dominas esta clase, podras resolver facilmente cualquiera de los derivados de la pendiente.

En conclusion...

Espero que nuestra clase haya sido de su agrado y le agradecemos por visitarnos y asi poder ayudarlos no se olviden de dar like y dejar sus comentarios para ayudarnos a mejorar. 

Mafer.

ECUACION DE LA RECTA

NOCHES DE ESTUDIO DC

AQUÍ DE NUEVO, con ustedes...la MUA

Hola, hoy les hablare de uno de mis temas preferidos de todo el universo; y no, no son "The Beatles". El tema de hoy es...

"ECUACIÓN DE LA RECTA"

Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano.

La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).

La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

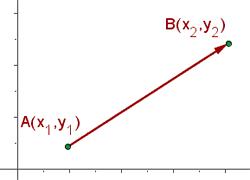
La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea  (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.

El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .

Entonces a breves terminos, proseguimos con la representacion:

1.– Ecuación general de la recta

2.– Ecuación principal de la recta

Sin mas, ahora se vienen los ejemplos:

Ejemplo 1:

m=3    b=10

y=3x+10 (que es la ecuacion que se pide)

Entonces, y-3x-10=0 la cual amplificamos por -1, quedando

-y+3x+10=0 para quedar

3x-y+10=0 como resultado de la ecuación.

Ejemplo 2:

Determina la ecuacion general de la recta de: P1=(4,3) P2=(-3,-2)

Asi que primero ya sabemos cual es la ecuacion de la recta que pasa por dos puntos y es:

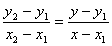
Reemplazamos:

–2 – 3 = y – 3
–3 – 4        x – 4

–5 = y – 3
–7        x – 4

y – 3  = x – 4 (–5 /–7)

y – 3 = –5 x  + 20
–7

–7 (y – 3) = –5 x + 20

–7y +21 + 5x – 20 = 0

5x – 7y + 1 = 0

Que se corresponde con una ecuación de la forma general

Ax + By + C = 0

Donde

A = 5

B = 7

C = 1

Eso es todo, como siempre, espero me hayan entendido y para mas comprension del tema, aqui les dejo con la obra maestra de Julioprofe, again.

https://www.youtube.com/watch?v=Jz8_omNLKTw

y

https://www.youtube.com/watch?v=wkuUEmA10BY

Los amo mas que a John Lennon, que sea una semana hermosa para todos, babay.

DISTANCIA ENTRE DOS PUNTOS

NOCHES DE ESTUDIO DC

Hola, que tal!!! 

El día de hoy les estaré explicando la clase de "Distancia entre dos puntos",  espero que puedan despejar todas sus dudas.

Aquí Vamos.

La distancia entre dos puntos equivale a la longitud del segmento de recta que los une, expresado numéricamente.

Dados dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa.

El Plano cartesiano se usa como un sistema de referencia para localizar puntos en un plano.

Otra de las utilidades de dominar los conceptos sobre el Plano cartesiano radica en que, a partir de la ubicación de las coordenadas de dos puntos es posible calcular la distancia entre ellos.

Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas (x2 – x1).

Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 - y2)

Ahora, si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación de estos.

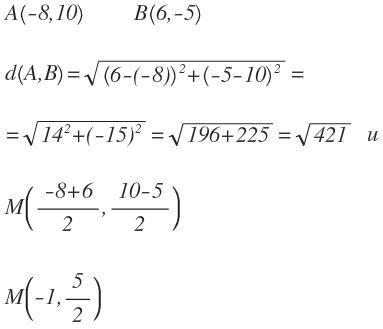
Espero que todo lo que he publicado les haya servido. Les dejo un vídeo de refuerzo por si las dudas.

https://www.youtube.com/watch?v=4NUsS6qkvv8&feature=youtu.be

 Esto es todo por hoy, nos vemos en la siguiente clase!!\

Majo <3

PRODUCTO PUNTO DE VECTORES

NOCHES DE ESTUDIO DC

¿QUIERO APRENDER?

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

Producto Punto de vectores

El producto escalar de dos vectores en un espacio vectorial es una forma bilineal, hermítica y definida positiva, por lo que se puede considerar una forma cuadrática definida positiva.

Más específicamente, es una aplicación cuyo dominio es V ² y su codominio es K, donde V es un espacio vectorial y K el conjunto de los escalares respectivo.[5]​ Esta aplicación amplía la oportunidad de emplear los conceptos de la geometría euclídeatradicional: longitudes, ángulos, ortogonalidad en dos y tres dimensiones. El producto escalar puede definirse también en los espacios euclídeos de dimensión mayor a tres, y en general en los espacios vectoriales reales y complejos. Los espacios vectoriales dotados de producto escalar reciben el nombre de espacios prehilbertianos.

Donde V {\displaystyle V\;}es un espacio vectorial y K{\displaystyle \mathbb {K} } es el cuerpo sobre el que está definido V{\displaystyle V\;}. La función (.,.) {\displaystyle \langle \cdot ,\cdot \rangle } (que toma como argumentos dos elementos de V {\displaystyle V\;}, y devuelve un elemento del cuerpo K {\displaystyle \mathbb {K} }) debe satisfacer las siguientes condiciones:

1. 1.     Linealidad por la izquierda:

(ax+by, z) = a (x, z)+b (y, z)

 {\displaystyle \langle ax+by,z\rangle =a\langle x,z\rangle +b\langle y,z\rangle }y linealidad conjugada por la derecha: {\displaystyle \langle x,ay+bz\rangle ={\overline {a}}\langle x,y\rangle +{\overline {b}}\langle x,z\rangle }

(x, ay + bz) = a (x, y) + b (x, z)

2.  Hermiticidad:

{\displaystyle \langle x,ay+bz\rangle ={\overline {a}}\langle x,y\rangle +{\overline {b}}\langle x,z\rangle }

3. Definida positiva:   si y sólo si x = 0

donde x,y,z{\displaystyle x,y,z\in V} € V son vectores de V,a,b  €  K {\displaystyle a,b\in \mathbb {K} }representan escalares del cuerpo K {\displaystyle \mathbb {K} } y c {\displaystyle {\overline {c}}}es el conjugado del complejo c.

Si el cuerpo tiene parte imaginaria nula (v.g., R) {\displaystyle \mathbb {R} }, la propiedad de ser sesquilineal se convierte en ser bilineal y el ser hermítica se convierte en ser simétrica.

También suele representarse por:

Un espacio vectorial sobre el cuerpo {\displaystyle \mathbb {R} } R o C{\displaystyle \mathbb {C} } dotado de un producto escalar se denomina espacio prehilbert o espacio prehilbertiano. Si además es completo, se dice que es un espacio de Hilbert. Si la dimensión es finita y el cuerpo es el de los números reales, se dirá que es un espacio euclídeo; si el cuerpo es el de los números complejos (y la dimensión es finita) se dirá que es un espacio unitario.

Todo producto escalar induce una norma sobre el espacio en el que está definido, de la siguiente manera:

En tal caso, esta es una de las infinitas normas que pueden ser generadas a partir de un producto interior.

Propiedades del producto punto

1 Conmutativa

2 Asociativa

3 Distributiva

4 El producto escalar de un vector no nulo por sí mismo siempre es positivo.

Ejercicio

Dados los vectores  y  hallar:

1.Los módulos de  y ·

2.El producto escalar de  y ·

3.El ángulo que forman.

4.El valor de m para que los vectores  y  sean ortogonales.

Si has llegado hasta aquí es porque necesitas clases de matemáticas urgentes.

Que tu cabeza sea donde se amontonan todas las riquezas del mundo.

Y…

Recuerda no puedes matar lo que no has creado, asi lo dijo Corey Taylor en una canción para Slipknot.

Nada♡

VECTORES

NOCHES DE ESTUDIO DC

Hola a todos, hoy veremos:

VECTORES

Primero empezaremos recordando el significado de vectores.

En física, un vector​ es un ente matemático como la recta o el plano. Un vector se representa mediante un segmento de recta, orientado dentro del espacio euclidiano tridimensional.

Y sus respectivos elementos...

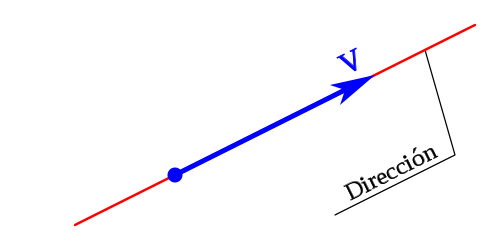
La dirección.

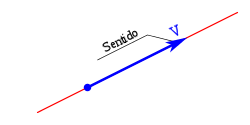
El sentido.

No olvidemos que el sentido se refiere exactamente a como va el mismo desde el punto A hasta el punto B.

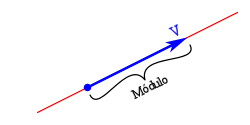
El modulo o la amplitud.

Es decir, en resumen, que el vector solo tiene tres partes fundamentales las mismas que son:

Nosotros, tenemos dos tipos de ejercicios preferidos con respecto al tema de los vectores, los mismos que tendrán un respectivo ejercicio demostrativo para que aprendan a resolverlos:

1. Suma de vectores.
2. Resta de vectores.

fuente del ejercicio, este mismo: areaciencias.com

 Ejercicio Suma de Vectores

 Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.

Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ? coseno 45º = ax/a; seno 45º = ay/a  ==> Despejando las componentes será:

ax= a cos⁡ 450

ay= a sen 450

Todo se vuelve mas sencillo para la calculadora ahora que procedemos a calcularlo luego de reemplazar los valores:

ax= 60 cos⁡ 450 = 60∙0.7= 42

ax= 42

ay= 60 sen⁡ 450 = 60∙0.7= 42

ay= 42

 Y si al finalizar del procedimiento las dos partes del ejercicio han salido con el mismo valor (como en este caso fue el numero 42), permiteme estrecharte la mano, porque has hecho un muy buen trabajo.

fuente del ejercicio, este mismo: areaciencias.com

Ejercicio Resta de Vectores

 Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2). ¿Cual será el vector resta de los dos?

  El vector AB = (-3 - 2) (4 - 2) = (-5, 2)  Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B. AB = (-5, 2)

Es decir, a cortas palabras solo tienes que hacer las restas (respetando la ley de los signos [ -.-=+ y +.-=-]) que se citan entre los paréntesis de A y B para resolver este tipo de ejercicio. Y here comes the sun.

Ahora un vídeo que te sera de ayuda y terminamos con nuestra clase.

https://www.youtube.com/watch?v=5E_V1j87YGM

Te pareció difícil esta clase de vectores? Déjanos tu comentario y haznos conocer tu opinión.

Quieres que la próxima clase trate de algún tema en especifico? No dudes en dejarnos tu propio titulo en los comentarios.

Bueno eso ha sido todo, hasta la próxima. 

saludos a toda la familia de la MUA.

INTRODUCCIÓN.

NOCHES DE ESTUDIO DC

QUIENES SOMOS?

Este blog fue realizado con el fin de transmitir a mas estudiantes como nosotros información de utilidad acerca de nuestra materia favorita, las Matemáticas.

Así que si has llegado ha esta pagina para aprender a buena hora porque con nuestros artículos semanales, saldrás mas matemática que el mismísimo Albert Einstein y pasaras el año rápidamente sin pisar el supletorio, porque recuerda amigue nunca es tarde para soñar. Ahora, sin mas preámbulos.

EMPECEMOS!!

Es hora de presentarnos!

Los Master Mister de las Matematicas:

• Valeria Aguirre, beatlemaniaca y dibujante con experiencia.
• Karelyn Guaman, calculadora humana y fanática de slipknot.
• Ruben Lopez, negociador experto y boxeador apasionado.
• Maria Jose Mera, corista y pianista por excelencia.
• Maria Fernanda Zambrano, amante de los deportes y experta en el arte de la vida.

Todos somos estudiantes del Domingo Comin con el propósito de transmitir un mensaje productivo de enseñanza.

Ahora que ya nos presentamos nosotros, solo faltas tu!