ECUACION DE LA RECTA

NOCHES DE ESTUDIO DC

AQUÍ DE NUEVO, con ustedes...la MUA

Hola, hoy les hablare de uno de mis temas preferidos de todo el universo; y no, no son "The Beatles". El tema de hoy es...

"ECUACIÓN DE LA RECTA"

Para entrar en esta materia y para entender lo que significa la Ecuación de la Recta es imprescindible estudiar, o al menos revisar, lo referido a Geometría analítica y Plano cartesiano.

La idea de línea recta es uno de los conceptos intuitivos de la Geometría (como son también el punto y el plano ).

La recta se puede entender como un conjunto infinito de puntos alineados en una única dirección. Vista en un plano, una recta puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

La línea de la derecha podemos verla, pero a partir de los datos que nos entrega la misma línea  (par de coordenadas para A y par de coordenadas para B en el plano cartesiano) es que podemos encontrar una expresión algebraica (una función) que determine a esa misma recta.

El nombre que recibe la expresión algebraica (función) que determine a una recta dada se denomina Ecuación de la Recta .

Entonces a breves terminos, proseguimos con la representacion:

1.– Ecuación general de la recta

2.– Ecuación principal de la recta

Sin mas, ahora se vienen los ejemplos:

Ejemplo 1:

m=3    b=10

y=3x+10 (que es la ecuacion que se pide)

Entonces, y-3x-10=0 la cual amplificamos por -1, quedando

-y+3x+10=0 para quedar

3x-y+10=0 como resultado de la ecuación.

Ejemplo 2:

Determina la ecuacion general de la recta de: P1=(4,3) P2=(-3,-2)

Asi que primero ya sabemos cual es la ecuacion de la recta que pasa por dos puntos y es:

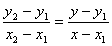
Reemplazamos:

–2 – 3 = y – 3
–3 – 4        x – 4

–5 = y – 3
–7        x – 4

y – 3  = x – 4 (–5 /–7)

y – 3 = –5 x  + 20
–7

–7 (y – 3) = –5 x + 20

–7y +21 + 5x – 20 = 0

5x – 7y + 1 = 0

Que se corresponde con una ecuación de la forma general

Ax + By + C = 0

Donde

A = 5

B = 7

C = 1

Eso es todo, como siempre, espero me hayan entendido y para mas comprension del tema, aqui les dejo con la obra maestra de Julioprofe, again.

https://www.youtube.com/watch?v=Jz8_omNLKTw

y

https://www.youtube.com/watch?v=wkuUEmA10BY

Los amo mas que a John Lennon, que sea una semana hermosa para todos, babay.