NOCHES DE ESTUDIO DC
Hola a todos, hoy veremos:
VECTORES

Primero empezaremos recordando el significado de vectores.
En física, un vector es un ente matemático como la recta o el plano. Un vector se representa mediante un segmento de recta, orientado dentro del espacio euclidiano tridimensional.
Y sus respectivos elementos...
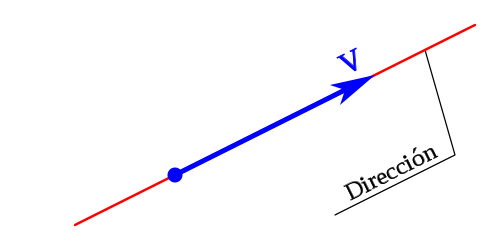
La dirección.
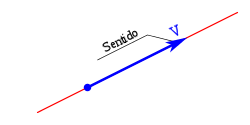
El sentido.
No olvidemos que el sentido se refiere exactamente a como va el mismo desde el punto A hasta el punto B.
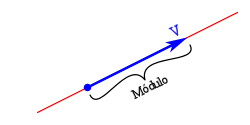
El modulo o la amplitud.
Es decir, en resumen, que el vector solo tiene tres partes fundamentales las mismas que son:

Nosotros, tenemos dos tipos de ejercicios preferidos con respecto al tema de los vectores, los mismos que tendrán un respectivo ejercicio demostrativo para que aprendan a resolverlos:

- Suma de vectores.
- Resta de vectores.
fuente del ejercicio, este mismo: areaciencias.com
Ejercicio Suma de Vectores
Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.
Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ? coseno 45º = ax/a; seno 45º = ay/a ==> Despejando las componentes será:
ax= a cos 450
ay= a sen 450
Todo se vuelve mas sencillo para la calculadora ahora que procedemos a calcularlo luego de reemplazar los valores:
ax= 60 cos 450 = 60∙0.7= 42
ax= 42
ay= 60 sen 450 = 60∙0.7= 42
ay= 42
Y si al finalizar del procedimiento las dos partes del ejercicio han salido con el mismo valor (como en este caso fue el numero 42), permiteme estrecharte la mano, porque has hecho un muy buen trabajo.
fuente del ejercicio, este mismo: areaciencias.com
Ejercicio Resta de Vectores
Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2). ¿Cual será el vector resta de los dos?
El vector AB = (-3 - 2) (4 - 2) = (-5, 2) Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B. AB = (-5, 2)
Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2). ¿Cual será el vector resta de los dos?
El vector AB = (-3 - 2) (4 - 2) = (-5, 2) Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B. AB = (-5, 2)
Es decir, a cortas palabras solo tienes que hacer las restas (respetando la ley de los signos [ -.-=+ y +.-=-]) que se citan entre los paréntesis de A y B para resolver este tipo de ejercicio. Y here comes the sun.
Ahora un vídeo que te sera de ayuda y terminamos con nuestra clase.
Te pareció difícil esta clase de vectores? Déjanos tu comentario y haznos conocer tu opinión.
Quieres que la próxima clase trate de algún tema en especifico? No dudes en dejarnos tu propio titulo en los comentarios.
Bueno eso ha sido todo, hasta la próxima.

saludos a toda la familia de la MUA.

