PRODUCTO PUNTO DE VECTORES

NOCHES DE ESTUDIO DC

¿QUIERO APRENDER?

Sólo tienes que dejarte guiar por mí verás como tu nota y tu tiempo libre subirán como la espuma.

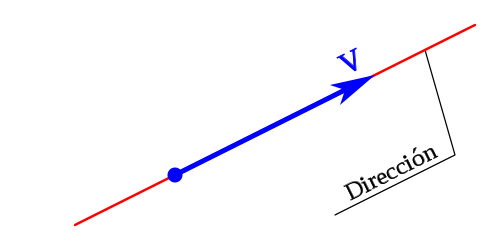
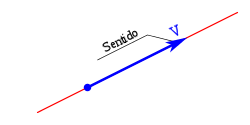
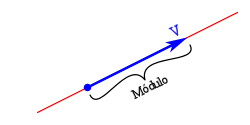
Producto Punto de vectores

El producto escalar de dos vectores en un espacio vectorial es una forma bilineal, hermítica y definida positiva, por lo que se puede considerar una forma cuadrática definida positiva.

Más específicamente, es una aplicación cuyo dominio es V ² y su codominio es K, donde V es un espacio vectorial y K el conjunto de los escalares respectivo.[5]​ Esta aplicación amplía la oportunidad de emplear los conceptos de la geometría euclídeatradicional: longitudes, ángulos, ortogonalidad en dos y tres dimensiones. El producto escalar puede definirse también en los espacios euclídeos de dimensión mayor a tres, y en general en los espacios vectoriales reales y complejos. Los espacios vectoriales dotados de producto escalar reciben el nombre de espacios prehilbertianos.

Donde V {\displaystyle V\;}es un espacio vectorial y K{\displaystyle \mathbb {K} } es el cuerpo sobre el que está definido V{\displaystyle V\;}. La función (.,.) {\displaystyle \langle \cdot ,\cdot \rangle } (que toma como argumentos dos elementos de V {\displaystyle V\;}, y devuelve un elemento del cuerpo K {\displaystyle \mathbb {K} }) debe satisfacer las siguientes condiciones:

1. 1.     Linealidad por la izquierda:

(ax+by, z) = a (x, z)+b (y, z)

 {\displaystyle \langle ax+by,z\rangle =a\langle x,z\rangle +b\langle y,z\rangle }y linealidad conjugada por la derecha: {\displaystyle \langle x,ay+bz\rangle ={\overline {a}}\langle x,y\rangle +{\overline {b}}\langle x,z\rangle }

(x, ay + bz) = a (x, y) + b (x, z)

2.  Hermiticidad:

{\displaystyle \langle x,ay+bz\rangle ={\overline {a}}\langle x,y\rangle +{\overline {b}}\langle x,z\rangle }

3. Definida positiva:   si y sólo si x = 0

donde x,y,z{\displaystyle x,y,z\in V} € V son vectores de V,a,b  €  K {\displaystyle a,b\in \mathbb {K} }representan escalares del cuerpo K {\displaystyle \mathbb {K} } y c {\displaystyle {\overline {c}}}es el conjugado del complejo c.

Si el cuerpo tiene parte imaginaria nula (v.g., R) {\displaystyle \mathbb {R} }, la propiedad de ser sesquilineal se convierte en ser bilineal y el ser hermítica se convierte en ser simétrica.

También suele representarse por:

Un espacio vectorial sobre el cuerpo {\displaystyle \mathbb {R} } R o C{\displaystyle \mathbb {C} } dotado de un producto escalar se denomina espacio prehilbert o espacio prehilbertiano. Si además es completo, se dice que es un espacio de Hilbert. Si la dimensión es finita y el cuerpo es el de los números reales, se dirá que es un espacio euclídeo; si el cuerpo es el de los números complejos (y la dimensión es finita) se dirá que es un espacio unitario.

Todo producto escalar induce una norma sobre el espacio en el que está definido, de la siguiente manera:

En tal caso, esta es una de las infinitas normas que pueden ser generadas a partir de un producto interior.

Propiedades del producto punto

1 Conmutativa

2 Asociativa

3 Distributiva

4 El producto escalar de un vector no nulo por sí mismo siempre es positivo.

Ejercicio

Dados los vectores  y  hallar:

1.Los módulos de  y ·

2.El producto escalar de  y ·

3.El ángulo que forman.

4.El valor de m para que los vectores  y  sean ortogonales.

Si has llegado hasta aquí es porque necesitas clases de matemáticas urgentes.

Que tu cabeza sea donde se amontonan todas las riquezas del mundo.

Y…

Recuerda no puedes matar lo que no has creado, asi lo dijo Corey Taylor en una canción para Slipknot.

Nada♡

VECTORES

NOCHES DE ESTUDIO DC

Hola a todos, hoy veremos:

VECTORES

Primero empezaremos recordando el significado de vectores.

En física, un vector​ es un ente matemático como la recta o el plano. Un vector se representa mediante un segmento de recta, orientado dentro del espacio euclidiano tridimensional.

Y sus respectivos elementos...

La dirección.

El sentido.

No olvidemos que el sentido se refiere exactamente a como va el mismo desde el punto A hasta el punto B.

El modulo o la amplitud.

Es decir, en resumen, que el vector solo tiene tres partes fundamentales las mismas que son:

Nosotros, tenemos dos tipos de ejercicios preferidos con respecto al tema de los vectores, los mismos que tendrán un respectivo ejercicio demostrativo para que aprendan a resolverlos:

1. Suma de vectores.
2. Resta de vectores.

fuente del ejercicio, este mismo: areaciencias.com

 Ejercicio Suma de Vectores

 Encuentra en forma analítica las componentes rectangulares de un vector cuyo módulo es de 60 y forma un ángulo de 45º con respecto a la horizontal en sentido noreste.

Datos
α = 450
sen 450= 0.7
cos 450= 0.7
ax ≈ ? coseno 45º = ax/a; seno 45º = ay/a  ==> Despejando las componentes será:

ax= a cos⁡ 450

ay= a sen 450

Todo se vuelve mas sencillo para la calculadora ahora que procedemos a calcularlo luego de reemplazar los valores:

ax= 60 cos⁡ 450 = 60∙0.7= 42

ax= 42

ay= 60 sen⁡ 450 = 60∙0.7= 42

ay= 42

 Y si al finalizar del procedimiento las dos partes del ejercicio han salido con el mismo valor (como en este caso fue el numero 42), permiteme estrecharte la mano, porque has hecho un muy buen trabajo.

fuente del ejercicio, este mismo: areaciencias.com

Ejercicio Resta de Vectores

 Tenemos las coordenadas del vector A que son ( – 3, 4) y la del vector B que son (4,2). ¿Cual será el vector resta de los dos?

  El vector AB = (-3 - 2) (4 - 2) = (-5, 2)  Hemos obtenido las coordenadas del vector suma de los dos anteriores el A y el B. AB = (-5, 2)

Es decir, a cortas palabras solo tienes que hacer las restas (respetando la ley de los signos [ -.-=+ y +.-=-]) que se citan entre los paréntesis de A y B para resolver este tipo de ejercicio. Y here comes the sun.

Ahora un vídeo que te sera de ayuda y terminamos con nuestra clase.

https://www.youtube.com/watch?v=5E_V1j87YGM

Te pareció difícil esta clase de vectores? Déjanos tu comentario y haznos conocer tu opinión.

Quieres que la próxima clase trate de algún tema en especifico? No dudes en dejarnos tu propio titulo en los comentarios.

Bueno eso ha sido todo, hasta la próxima. 

saludos a toda la familia de la MUA.

INTRODUCCIÓN.

NOCHES DE ESTUDIO DC

QUIENES SOMOS?

Este blog fue realizado con el fin de transmitir a mas estudiantes como nosotros información de utilidad acerca de nuestra materia favorita, las Matemáticas.

Así que si has llegado ha esta pagina para aprender a buena hora porque con nuestros artículos semanales, saldrás mas matemática que el mismísimo Albert Einstein y pasaras el año rápidamente sin pisar el supletorio, porque recuerda amigue nunca es tarde para soñar. Ahora, sin mas preámbulos.

EMPECEMOS!!

Es hora de presentarnos!

Los Master Mister de las Matematicas:

• Valeria Aguirre, beatlemaniaca y dibujante con experiencia.
• Karelyn Guaman, calculadora humana y fanática de slipknot.
• Ruben Lopez, negociador experto y boxeador apasionado.
• Maria Jose Mera, corista y pianista por excelencia.
• Maria Fernanda Zambrano, amante de los deportes y experta en el arte de la vida.

Todos somos estudiantes del Domingo Comin con el propósito de transmitir un mensaje productivo de enseñanza.

Ahora que ya nos presentamos nosotros, solo faltas tu!